in honor of tau

Note: this blog was originally written on the MIT Admissions Blog here. Because of things like footnotes and images, it’s best you read it on that site! This page will redirect you in 10 seconds.

---

In honor of blog post number 6283≈1000τ, I’ve decided to do a post dedicated to my favorite number. Here, τ (the Greek letter tau, usually pronounced to rhyme with how but some people rhyme it with law) refers to the superior circle constant, τ=6.283…=2π. And I cannot help but tell you about the glory that is tau, alongside a few anecdotes about tau, MIT, and myself c:

proof that this is the post number i claim it was

why tau?

Note: This section gives an introduction to tau from the ground up. The only thing needed to understand everything is calculus, but if you haven’t taken that yet, this section should still be accessible⁠01 even with just algebra/geometry (hopefully). Much of the material from this section is drawn from Michael Hartl’s The Tau Manifesto. I encourage you to read it for a deeper, more involved read about tau!

Pi, or 3.14159…, or π, is perhaps the single most iconic mathematical object. From the t-shirts with pi to Pi Day celebrations on March 14th to the Simpsons, even. Pi is a number that relates two important parts of circles: their circumference (length around the circle) and diameter (length across the circle). The ratio of every circle’s circumference to its diameter is exactly pi: in other words, π=Cd.

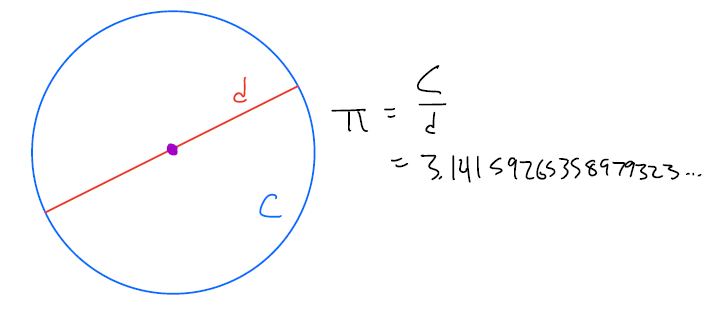
all diagrams are drawn by yours truly on my mit ipad. i apologize for my terrible handwriting

But should we use a diameter for our circle constant? After all, most geometry classes introduce circles as

circle noun: a shape that is made of of the set of all points that are a fixed distance away (the radius) from a single point (the center)

or something similar.

Most notably, we don’t define a circle by the length across it, but instead by its radius — half of that. The reason for this is deeper than a standard dictionary definition: there are many shapes (such as the Reuleaux triangle) that have a constant width, but a circle is the only two-dimensional figure for which all points on the boundary are the same distance from a center.

So perhaps it’s better to use a different circle constant: one that relates a circle’s circumference and its radius.

Doing a bit of algebra on the definition of π, and using the fact that a diameter d is twice the radius r (and so d/2=r) we get

2π=2Cd=Cd/2=Cr.

And so 2π gets at an even more fundamental relationship that is present in circles — the relationship between the circumference and the radius. For convenience, let’s denote 2π as τ.

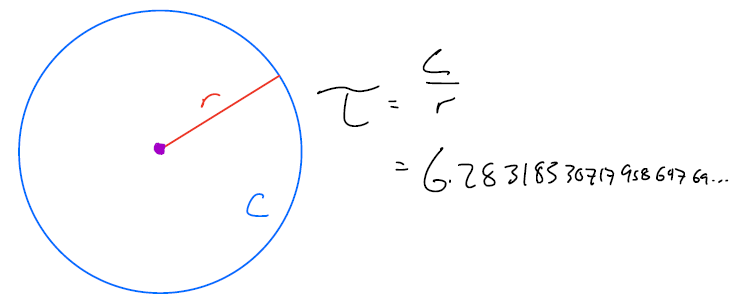
This idea that pi isn’t truly “fundamental” has been talked about for a long time. Michael Hartl wrote the first version of The Tau Manifesto for Tau Day (June 28th) in 2010. Nine years earlier, Bob Palais wrote a 3-page article titled “π is wrong!” in a mathematical newsletter. But before just blindly accepting that τ>π (true by definition — a tau-tology, if you will), it’s important to understand other places that π is used besides the circumference of a circle.

If you’re familiar with geometry, you might be incredibly hesitant about τ because of the formula for a circle’s area:

A=πr2=12τr2.

This formula, at first glance, looks much uglier with tau than with pi, with a constant factor of 12 sticking out front.

If you’re taking a physics class right now, the form of the area equation with tau might look quite familiar to you. A few examples:

• Δx=12at2 is the formula for the distance traveled Δx by an object that starts at rest and accelerates at a rate of a for a time of t.
• Ek=12mv2 is the kinetic energy Ek possessed by an object with mass m traveling with velocity v.
• Es=12k(Δx)2 is the potential energy Es stored in a spring with a spring constant of k that is displaced from equilibrium by a distance of Δx.

With these in mind, the factor of 12 looks a lot less weird in front of there. But it’s not just a surface similarity: the 12 exists in front of all of these equations for the same reason: the integral⁠02 ∫xdx=12x2.

One way to “derive” the formula for the area of a circle is by taking the areas of thin rings in the circle (imagine an onion with many layers). If we find the area of each of these rings, and add them all up together, we can get the area of the circle!

But what’s the area of one of these rings? If some ring that’s r′ out from the center has a thickness of dr′, we can imagine “unrolling” it into a rectangle, and we can pretty easily see that it has a height of dr′ and a width of the “circumference” of the ring, or τr′. Then, its area is simply τr′dr′.

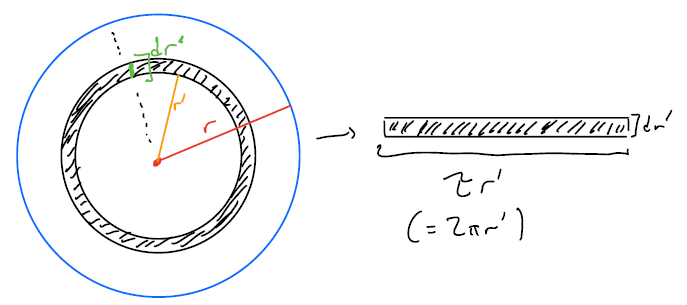
So, we can add up each of these areas (τr′idr for each ring i, and so ∑iτr′idr in total), and we’ll get the area of the circle! However, this sum is an approximation — but it’ll get more exact when the rings get smaller: i.e., dr′→0. When we do that, calculus students may realize that our sum turns into an integral, and we simply need to evaluate

∫r0τr′dr′=12τr2

and the 12 pops out — not by magic, but because of the power rule for integrals and the relationship of the area of a circle and its circumference.

Each of the equations above with factors of 12 can be represented as some integral, a sum of “smaller things”:

• Integrating velocity v=at with respect to time gives Δx=∫vdt=∫atdt=12at2
• Integrating momentum p=mv with respect to velocity gives Ek=∫pdv=∫mvdv=12mv2
• Integrating spring force F=kΔx with respect to the Δx gives Es=∫kdΔx=∫kΔxdΔx=12k(Δx)2

And so now we have a second piece of evidence for tau: its use in the area formula.

Reason number 3⁠03 is incredibly useful if you’re taking trigonometry/pre-calculus right now, there’s one incredibly useful reason to use tau instead of pi: its use in radians. If you’re unfamiliar with those subjects, the most important thing to know is that radians, like degrees, are a way of measuring angles, with the conversion rate 180∘=πradians. Below is an image with this conversion represented on two unit circles.

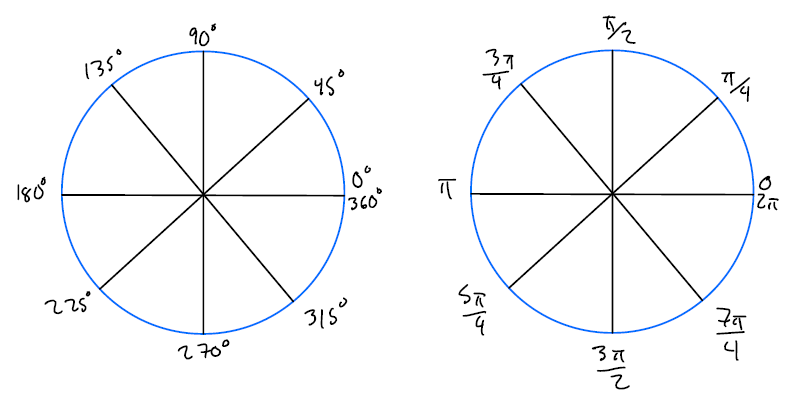
Radians are often troubling pedagogically; whenever you learn them, it’s often very hard to wrap your head intuitively around degree-to-radian conversions, what a radian actually means,⁠04 and other general confusion. If someone tells you that something is π/3 radians, how many is that? It’s a third of a semicircle, 180∘, which makes it a sixth of a circle, or 360∘/6=60∘. Lots of steps, lots of room for silly mistakes, lots of room for head-scratching.

Now consider a unit circle, but with the angles denoted as multiple of τ:

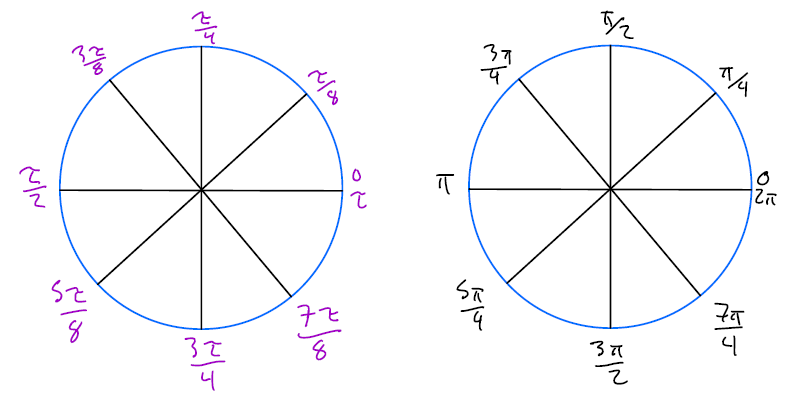
Now, the numbers make much more sense. Since tau is symbolized by a Greek “t”, we can imagine that τ stands for “turn”; one turn around the circle is exactly τ radians! Now, conversions between angles and degrees are easy: one-eighth of a circle, or 45∘, is exactly 18τ. Boom, angles and radians much easier. (I still sometimes convert radian angles given in terms of π to τ so that I can work with them more easily.)

Not only is this helpful for understanding unit circle mechanics and conversions, but the usefulness of tau here extends to all trigonometric functions (sine, cosine, secant, cosecant all have periods of τ). So useful indeed c:

This section is already going on a bit longer than I anticipated,⁠05 so here’s a hodgepodge of various other places where you can use tau!

• The probability density function for the normal distribution with mean 0 and standard deviation 1 (the classic “bell curve”) is given by 1τ√e−12x2.
• Euler’s identity (eiπ=−1) becomes much more elegant if we square both sides, which then can be expressed in terms of tau: eiτ=1.
• The reduced Planck constant ℏ is given by ℏ=hτ.
• Stirling’s approximation for the factorial function is given by n!∼τn−−√(ne)n .
• Cauchy’s integral formula states that given a holomorphic function f on the complex plane C and a disc D which has positively oriented boundary of γ, every point a in the interior of D satisfies f(a)=1τi∫γf(z)z−adz.

If you’re interested in more: as I stated above, the material here is largely drawn from The Tau Manifesto by Michael Hartl. I highly encourage reading through it for more tau-related arguments (with math that is deeper than this post) and rebuttals to counterarguments proposed by the Pi Manifesto (which was written in response to The Tau Manifesto :P).

Since The Tau Manifesto was published, there has been an incredible growth of support for a new circle constant. To get an idea of the scale of this, peek through The State of the Tau. Some personal highlights include:

• SMBC and XKCD comics referencing tau
• PEP 628 added tau to Python’s official math library
• Multiple references to MIT

That last bullet point transitions nicely into…

tau, mit history

As one might expect, an institution like MIT, home to many a math nerd, has a few fans of the superior circle constant.⁠06 Here’s a few ways in which tau has made an appearance at MIT.

• MIT students are known for their

  hacks

  pranks and jokes that students pull, often by putting objects in places that they shouldn’t be. In 1979, some MIT students stuck a (plastic) cow on top of the Great Dome.

  

  cow on dome! from mit museum

  This cow was stolen from Hilltop Steak House in Saugus; later, Hilltop donated an extra plastic cow to the MIT Museum exhibition to commemorate the hack. This cow now sits inside of Stata, nearby to other hacks (such as the police car and Collier’s Cranes).

  On Tau Day 2015, the hack exhibit itself was hacked: some MIT students decorated the cow with tau-associated memorabilia in an exhibit dubbed “Tau on the Cow”. Check out the MIT Hack Gallery for some photos and more information about the hack!

• Four fraternities at MIT (under the MIT Interfraternity Council) have “Tau” in them: Delta Tau Delta, Tau Epsilon Phi (coed), Theta Tau, and Zeta Beta Tau. The Number Six Club (Delta Psi) is the Tau Chapter, and the fraternity Delta Kappa Epsilon is the Sigma Tau Chapter. Two honor societies at MIT have tau in them: Tau Beta Pi (engineering honor society) and Pi Tau Sigma (mechanical engineering honor society). The second floor of the west parallel of East Campus is named Putz, which sometimes goes by Pi Tau Zeta.
• MIT Admissions has recently been releasing its decisions at 6:28 PM ET on Pi Day.⁠07 This happened for the first time in 2012, when Sir Nigel Blogberry announced some SMASHING news! in a post that is so incredible that you absolutely need to read it. Matt McGann ‘00, former director of admissions, wrote a very short post that year acknowledging the tau vs. pi debate. All good times.

tau, my history

I first encountered tau somewhere around 2013, just when I was starting high school. I’m not exactly sure where, but I suspect that it was a Vihart video.

I intended for this section to be a lot longer to talk about lots of things with myself and tau: but I’m limited by the fact that 1) I entered high school literally 8 years ago, and remembering things from back then is very, very hard, and 2) I don’t have any photos from that time.⁠08 So instead, here’s a few anecdotes about me and tau from way back when.

• My freshman year, someone in my math club gave me the nickname Tau-lo. It stuck around. One of my friends from high school still calls me Taulo everytime she sees me.
• Tau was (and continues) to be a part of a lot of my online identity: Gmail profile picture, parts of my names on many platforms, etc. I’m currently considering changing my default username on sites, and many of my ideas still involve tau…
• Searching through my Google hangouts chat history gives me hundreds of messages just about tau. Granted, some of these are non-math uses of tau (like for the time constant of RC circuits) but many of them are just people getting my attention in a groupchat or talking about the number.
• At some point in high school, I had 100 digits of tau memorized and only a handful of pi digits memorized. That changed in my senior year, where as a part of my school’s math club, I judged the pi-reciting contest. I ended up accidentally learning a lot more digits of pi because I had to keep checking if people were saying pi correctly. Sigh.
• At ARML 2017, my team was playing a mafia game with a few other friends from other regions (including some that are at MIT now). I moderated a 15-person game of mafia, themed as the tau-n vs. the pi-mafia, and it ended 3 people and a confirmed τ-nsperson needing to guess the last member of the pi-mafia with basically no information. (Rinik K. ’21 and Freya E. ’23 were there to witness the glory of that game.)

I tried to pack light when coming to Cambridge this year, so my tau shirt is currently stowed away in a box back at home, alongside many other shirts that I haven’t worn in a while. But come June 28th,⁠09 I promise that I will be putting that shirt back on to celebrate and spread the glory of τ.

Direct Link